MULTIPLICAÇÃO DE MATRIZES


PROPRIEDADES
a) A multiplicação de matrizes não é comutativa, isto é, para duas matrizes quaisquer A e B é falso que AB = BA necessariamente.


TIPOS DE MATRIZES
MATRIZ QUADRADA
A matriz constituída pelo mesmo número de linhas e colunas é chamada matriz quadrada.
Assim, uma matriz constituída por n linhas e n colunas é uma matriz quadrada de ordem n × n ou simplesmente uma matriz quadrada de ordem n.

MATRIZ-LINHA
É toda matriz de ordem 1 × n, ou seja, que possui uma única linha.

MATRIZ COLUNA
É toda matriz de ordem m × 1, ou seja, que possui uma única coluna.

MATRIZ NULA
É toda matriz que possui todos os seus elementos iguais a zero.

A matriz nula é o elemento neutro da adição de matrizes, assim A + 0 = A e 0 + A = A.
MATRIZ DIAGONAL
É toda matriz quadrada em que os elementos não pertencentes à diagonal principal são iguais a zero, ou seja, aij = 0 sempre que i ≠ j.

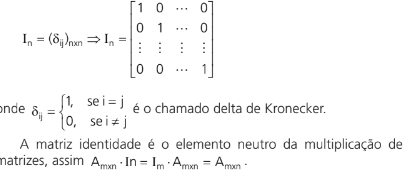
MATRIZ IDENTIDADE
É a matriz diagonal, na qual todos os elementos da diagonal principal são iguais a 1.
MATRIZ TRIANGULAR SUPERIOR
Chama-se matriz triangular superior, à matriz quadrada que possui todos os elementos abaixo da diagonal principal nulos.

MATRIZ TRANSPOSTA

PROPRIEDADES

MATRIZ SIMÉTRICA
Uma matriz quadrada diz-se simétrica quando aij = aji para todo 1 ≤ i, j ≤ n, ou seja, quando é igual à sua matriz transposta.
Daí resulta que os elementos simétricos em relação à diagonal principal são iguais.

MATRIZ ANTI-SIMÉTRICA

MATRIZES COMUTATIVAS
Como já visto no anteriormente, em geral, AB ≠ BA.
Se A e B matrizes quadradas e de mesma ordem, diz-se que A e B comutam, quando ocorre AB = BA.
A e B comutam ⇒ AB = BA
MATRIZES ANTICOMUTATIVAS
Se A e B matrizes quadradas e de mesma ordem, diz-se que A e B são anticomutativas, quando ocorre AB = −BA.
A e B são anticomutativas ⇒ AB = −BA
MATRIZ INVOLUTIVA

MATRIZ IDEMPOTENTE
Matriz singular é a matriz quadrada cujo determinante é nulo.
A é singular ⇒ det A = 0
Matriz não-singular é a matriz quadrada cujo determinante é diferente de zero.
A é não-singular ⇒ det A ≠ 0
MATRIZ INVERSÍVEL

PROPRIEDADES

MATRIZ ORTOGONAL
Uma matriz é dita ortogonal quando sua transposta e sua inversa coincidem.

MATRIZ COFATORA
A matriz cofatora de uma matriz quadrada A, indicada comumente por A’, é outra matriz quadrada cujos elementos são os cofatores dos elementos correspondentes da matriz A. No próximo módulo aprenderemos a calcular os cofatores de uma matriz.
No próximo módulo aprenderemos a calcular os cofatores de uma matriz.
MATRIZ ADJUNTA
A matriz adjunta de uma matriz quadrada A, comumente indicado por A, é a transposta da matriz dos cofatores.
MATRIZES SEMELHANTES
Duas matrizes A e B são ditas semelhantes, se existir uma matriz não singular P tal que

CÁLCULO DA MATRIZ INVERSA
É possível obter a inversa de uma matriz a partir da sua definição como no exemplo abaixo:

Esse método é muito trabalhoso, principalmente para matrizes de maior ordem. Vamos então desenvolver outros métodos para a obtenção da matriz inversa
OBTENÇÃO DA MATRIZ INVERSA USANDO DETERMINANTES
COFATOR

MATRIZ DOS COFATORES
Seja M uma matriz quadrada de ordem n. A matriz dos cofatores M’ é a matriz obtida a partir de M, substituindo cada elemento pelo seu cofator.

MATRIZ ADJUNTA
Seja M uma matriz quadrada de ordem n e M’ a matriz dos cofatores de M, a matriz adjunta de M, indicada por M, é a transposta da matriz M’.

MÉTODO DA ELIMINAÇÃO DE GAUSS
OPERAÇÕES ELEMENTARES COM FILAS
Denominam-se operações elementares com las em uma matriz às três seguintes operações:
a. permutação de duas las quaisquer;
b. multiplicação de uma la por um escalar; e
c. substituição de uma linha pela sua soma com outra
multiplicada por um escalar não-nulo.
MATRIZES EQUIVALENTES
Duas matrizes A e B de mesma ordem são equivalentes, indicado por A~B, quando uma é obtida da outra por meio de uma seqüência de operações elementares.
DETERMINAÇÃO DE MATRIZES INVERSAS PELO MÉTODO DE ELIMINAÇÃO DE GAUSS
Esse método consiste em colocar uma matriz identidade ao lado da matriz considerada. Em seguida, efetuam-se as mesmas operações elementares nas las de ambas as matrizes até que a matriz A tenha
sido reduzida à matriz identidade. A matriz identidade sobre a qual foram efetuadas as operações elementares será convertida, então, na matriz inversa de A.
Observemos a aplicação desse método no exemplo a seguir:




